Now I'm good with Physics, but our professor has been on vacation for a week, and we got two different subs, who didn't cover the topic... I am doing some homework, and there is this problem...
A Coast Guard cutter detects an unidentified ship at a distance of 19.4 km in the direction 17.8° east of north. The ship is traveling at 27.3 km/h on a course at 39.4° east of north. The Coast Guard wishes to send a speedboat to intercept the vessel and investigate it. If the speedboat travels 48.9 km/h, in what direction should it head? Express the direction as a compass bearing with respect to due north.
Now I have no idea how to begin to tackle this problem. Does anyone have some experience in solving these types of problem? What are the underlying concepts that should be used to solve this problem?
Physics problem
It's just a calc problem. Draw two right triangles to start, and remember that velocity = d/dt [displacement].
Assume the coast guard vessel is at (0, 0). You can easily figure out the position of the unidentified ship using trig. Draw a right triangle with a vertex at the origin and legs going north and east; 17.8 degrees is the angle between due north and the unidentified ship's position with respect to that of the CG vessel. so 19.4 km * sin(17.8 deg) = unidentified ship's X position, and 19.4 km * cos(17.8 deg) = unidentified ship's Y position. Then you have its velocity in a given direction (you can use trig again to figure out the megnitude of the X and Y components of this vector) and you need to solve for the angle from the origin at which a ship traveling at 48.9 km/h will reach the unidentified ship. If you want, you can figure out the equations for those lines and find their point of intersection, or you can use one of the Newtonian formulas for each ship, set them equal to each other, and that will give you the answer.
Assume the coast guard vessel is at (0, 0). You can easily figure out the position of the unidentified ship using trig. Draw a right triangle with a vertex at the origin and legs going north and east; 17.8 degrees is the angle between due north and the unidentified ship's position with respect to that of the CG vessel. so 19.4 km * sin(17.8 deg) = unidentified ship's X position, and 19.4 km * cos(17.8 deg) = unidentified ship's Y position. Then you have its velocity in a given direction (you can use trig again to figure out the megnitude of the X and Y components of this vector) and you need to solve for the angle from the origin at which a ship traveling at 48.9 km/h will reach the unidentified ship. If you want, you can figure out the equations for those lines and find their point of intersection, or you can use one of the Newtonian formulas for each ship, set them equal to each other, and that will give you the answer.
What the heck are you talking about? It's simple trig.DCrazy wrote: It's just a calc problem. Draw two right triangles to start, and remember that velocity = d/dt [displacement].
Assume the coast guard vessel is at (0, 0). You can easily figure out the position of the unidentified ship using trig. Draw a right triangle with a vertex at the origin and legs going north and east; 17.8 degrees is the angle between due north and the unidentified ship's position with respect to that of the CG vessel. so 19.4 km * sin(17.8 deg) = unidentified ship's X position, and 19.4 km * cos(17.8 deg) = unidentified ship's Y position. Then you have its velocity in a given direction (you can use trig again to figure out the megnitude of the X and Y components of this vector) and you need to solve for the angle from the origin at which a ship traveling at 48.9 km/h will reach the unidentified ship. If you want, you can figure out the equations for those lines and find their point of intersection, or you can use one of the Newtonian formulas for each ship, set them equal to each other, and that will give you the answer.
See this diagram:
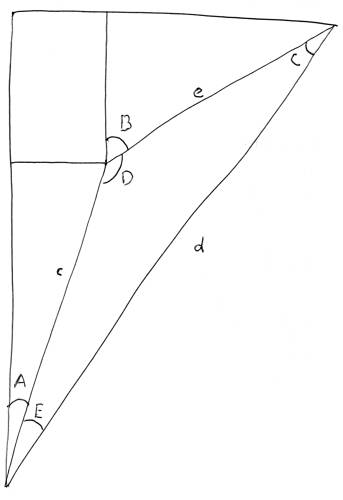
A = Angular direction of unidentified ship.
B = Angular course of unidentified ship.
c = Distance of unidentified ship.
d = Distance the speed boat travels before intercepting.
e = Distance unidentified ship travels before being intercepted.
A+E = Direction the speedboat should head to intercept.
A = 17.8°
B = 39.4°
c = 19.4 km
d/e = (48.9 km/h)/(27.3 km/h)
d = 1.72e
D = 180°-B+A
D = 158.4°
Law of Sines:
sin(E)/e = sin(D)/d
sin(E)/e = sin(D)/1.72e
sin(E) = sin(D)/1.72
E = arcsin(sin(D)/1.72))
E = arcsin(sin(158.4°)/1.72))
E = 12.36°
A+E = 30.2°
Re:
If I forget about the law of sines, I'll just derive it and then use it anyway.DCrazy wrote:Forgot about the Law of Sines. Without it, you need to figure out where the unidentified ship will be when the Coast Guard ship intercepts it: v = dx/dt => x = vt.
The problem is asking us to figure out the angle we need to point the speedboat to intercept the unidentified ship. You don't need any calculus for any of that. You don't need any calculus to figure out the position of the speed boat either... if that's what we wanted... which it isn't.
It's triangulation man... triangulation!



