DescentBB

Perhaps you've seen this. ... I just did the other day. But there are a number of math geeks here that might appreciate this....

Heh, the text on that is completely wrong. The middle term is e raised to the i times Pi, not 2 times Pi, and therefore comes out to -1. That check is from the author of the webcomic xkcd; the joke is that Verizon apparently billed him for .2 cents, so he decided to have some fun with writing the check.

I knew I could count on you guys!

http://xkcd.com/verizon/
The recording of the encounter with customer service is unbelievable. I actually sat and listened to the whole thing (it's rather long). You can really share George Vaccaro's frustration. It really did change my opinion of Verizon, haha.

Oh dear lord. I just learned what sequences and series were, and how to work them out.

Had some fun indeed.

._.

edit: though I do know that the series in there simply converges to 1.
So the whole thing is just 0.002 - 1 + 1

Along the lines of fun ways to express the number one.....



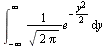
Nerd points to the first person to identify the equation (Foil, Lothar, Drakona?)

Integrating over the pdf of the standard normal distribution.

outside surface area of a sphere?

Jeff's right. Woo Jeff!

I sort of cheated. It looked like a normal distribution, but I didn't recognize it as the standard normal distribution until I looked up normal distributions in wikipedia.

You can apply the equation to any normal distribution by manipulating the range over which you integrate... my textbook is at home but you'd integrate from -infinity to x, where x is determined based on your endpoint, mean, and variance.

Are you sure you're not talking about just evaluating the cdf at value x? This is the definition of the cdf for any pdf. If you look up the general normal distribution in wikipedia, you can see the parameters mu and sigma (mean and variance). In the standard normal distribution, mu=0 and sigma=1, simplifying somewhat.