DescentBB

Posted: **Thu Nov 03, 2011 6:20 pm**

Here's an interview question a friend of mine got recently. Suppose you have a list/array of elements...

[a_1, a_2, ..., a_n, b_1, b_2, ..., b_n]

Give an in-place algorithm to reorder the elements to have positions

Code: Select all

[a_1, b_1, a_2, b_2, ..., a_n, b_n]

that requires only O(n) time.

The data in the array is arbitrary. In other words, after you move elements around, you cannot recognize that an element is, say, a_3 without using space to keep track of that.

My friend, over the phone, gave an algorithm* that required O(n*log(n)) time. Can anyone think of a O(n) algorithm? (Or, if perhaps the interviewers are devious, prove the problem requires ω(n) time?)

*His algorithm is swap the array to

Code: Select all

[a_1, b_1, a_3, b_3, ..., a_{n-1}, b_{n-1}, a_2, b_2, a_4, b_4, ..., a_n, b_n]

Now consider the block [a_1, b_1] -> a_1; [a_2, b_2] -> b_1; [a_3, b_3] -> a_2; [a_4, b_4] -> b_2; etc. Now recursively perform this algorithm again on these blocks until the entire array is a single block. Since each iteration requires O(n) swaps and there will be overall O(log(n)) iterations (since, each round, the block size doubles and the number of blocks is halved), this takes O(n*log(n)) time.

Posted: **Thu Nov 03, 2011 10:06 pm**

This looks easy, but I've probably missed something. I'll take a crack at it soon.

Posted: **Thu Nov 03, 2011 10:16 pm**

The in-place part is what makes this problem difficult. In this case, it means that you can't solve it by creating, say, a new list, and then just copying them into that one in the right order. You can only swap them around in the list that you're given, plus use a constant amount of temporary variables.

Posted: **Thu Nov 03, 2011 10:53 pm**

Your wikipedia link references a swap command, is that permissible?

Can you do:

reorganize()
for i from 1 to n/2
swap(n/2+i, 2i)

?

Posted: **Thu Nov 03, 2011 11:18 pm**

You can use swaps, since they only require a constant amount of temporary variables. Your algorithm doesn't work though... what will the list look like after a few iterations?

Posted: **Fri Nov 04, 2011 11:00 am**

Something that I don't know would work: start at a_2 and start swapping each element into its final location (if you know the initial, you know the final), swapping the element it replaces into its final location, and so on recursively. This would pretty much climb up through the array until it ran out of elements. The complication is that you'll need to do this multiple times since I'm pretty sure it'll miss elements at first, and you need some algorithmic way of knowing whether an element has already been swapped or not.

Posted: **Fri Nov 04, 2011 11:51 am**

assuming that each group is already sorted; then what Sirius and snoopy propose will work(snopy's example code is a bit off).

if you are using c/c++ there is a O(n) method to do it, but its not in-place.

Posted: **Fri Nov 04, 2011 12:57 pm**

This brings up something that I need to get clarified this afternoon, which is whether you can identify an element's original position (e.g., that it's "a_3") inherently, regardless of its current position in the array, without requiring any extra space to keep track of that. Assuming that you can do this might be cheating. If so, that would invalidate trivial solutions like mine to just heap sort it, whereas my friend's algorithm given at the bottom of my original post would still work, albeit still in too much time.

Snoopy's algorithm can't fall into the above issue, and it's clearly in place and terminates in O(n) time, but it just doesn't return the correct results, and I don't see how any trivial modification would fix it. However, you're welcome to prove me wrong.

Sirius's might run into the above issue. If it turns out not to be an issue, then showing that it's O(n) would be the next step... it looks like it *could* be as bad as, but no worse than, \Theta(n^2), since you would never need more than n passes. But I should clarify my original issue before we put too much more thought into this.

Posted: **Fri Nov 04, 2011 5:31 pm**

Ack, so the problem is harder. You can't look at an element in the array and tell that it's e.g. "a_3" without using some space to keep track of that. So the data in the array itself is arbitrary. I'll edit my original post to clarify this issue.

Posted: **Fri Nov 04, 2011 5:34 pm**

Okay, I see what you mean.

a1, a2, a3, a4, ...., an, b1, b2, b3, b4, ... , bn

to

a1, b1, a2, b2, a3, b3, ....., an, bn

two mistakes: the list is 2n long, not n/2 long. My idea would generate:

a1, b1, a3, b2, a5, b3,..... , a2, a4, a6, a8, etc.

So, let me see if I can break it down:

a1 stays in place, b1 moves by (1-n), a2 moves by 1, b2 moves by (2-n), a3 moves by 2, b3 moves by (3-n).

I one solution probably lies in vacating one spot, then re-arranging by always filling appropriate spot, and finally filling the last open spot, but that takes 2n time.

I bet your friend is along the right track, where you swap by blocks. I'd bet the key (if it's doable) is to start with a swap of single elements in such a way that you can then swap blocks of two elements, then three, and so on to n. Making myself a picture.....

Posted: **Fri Nov 04, 2011 5:41 pm**

If you're not familiar with asymptotic notation, 2*n = O(n). Basically, the function has to be asymptotically <= c*n as n gets large, where c is some constant that is not a function of n. So I would be more concerned with the correctness of the solution.

Posted: **Fri Nov 04, 2011 6:36 pm**

darn need for contiguous blocks.

Posted: **Fri Nov 04, 2011 6:56 pm**

I have the solution.

Made myself a spreadsheet and figured it out.

reorganize()
for i from 1 to n/2
swap(2i, (2i)+(n-1))
for i from 1 to n/2-1
swap([2i+1...n], [n+1...2n-2i]

Essentially: start by swapping a2 & b1, a4 & b3, .... an & bn-1

you end up with:

a1, b1, a3, b3, a5, b5, ...., an-1,bn-1, a2, b2, a4, b4, ....., an, bn

Then, you swap down the middle everything except for you outer pairs, recursively working your way inward from both sides by a pair at a time.

Posted: **Fri Nov 04, 2011 7:02 pm**

Note that for my notation the array is 2n long.

Posted: **Fri Nov 04, 2011 7:17 pm**

Cool.

snoopy wrote:Then, you swap down the middle everything except for you outer pairs, recursively working your way inward from both sides by a pair at a time.

Could you explain this step more? My friend's O(n*log(n)) solution is basically yours up until this point, but this is where I no longer follow yours.

Posted: **Fri Nov 04, 2011 9:29 pm**

Sorry, I wrote the explanation quickly. I also messed up the if statements in that they only need to run to n/2 and n/2-1. I edited the earlier port to that effect. A picture is worth a thousand words... see below: The green boxes are what gets swapped. I arbitrarily went up to 10.

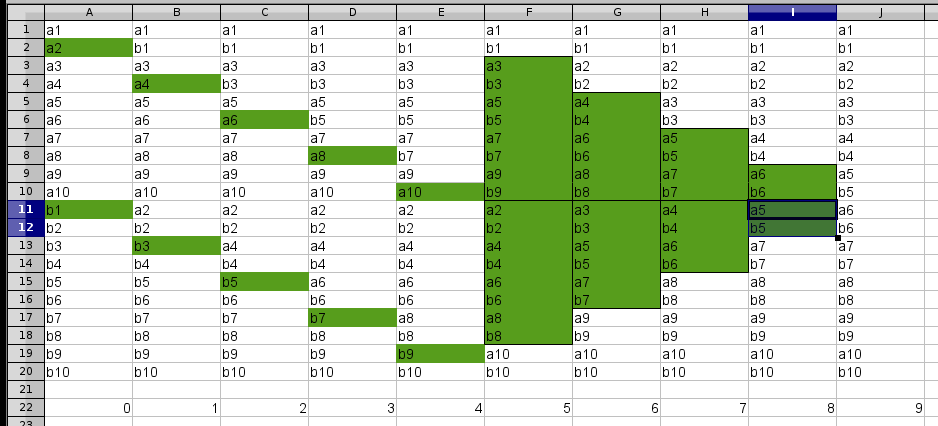
Your friend starts down the same track as did, but instead of recursively running the same scheme again, I changed up the scheme for the second portion, which maybe I didn't need to have done.

I could have handled it all with the second method (I'm not quite sure why I saw it on the second portion, but not the first.

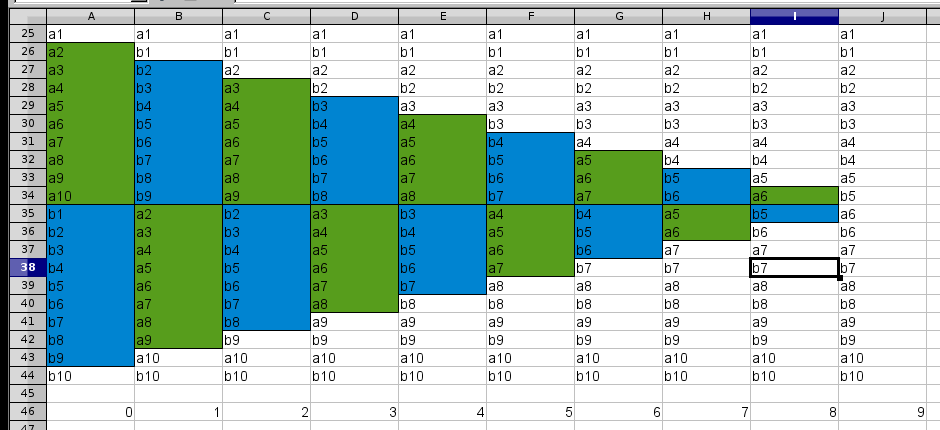
Something like this:

rearrange()
for i from 1 to n-1
swap([i+1...n], [n+1...2n-i]

And a picture:

Posted: **Fri Nov 04, 2011 9:32 pm**

That was a fun little challenge.

Hope your friend lands the job.

Posted: **Fri Nov 04, 2011 9:47 pm**

But if you're doing, on average, n/2 swaps on each of n rounds, then this is n*n/2 = \Theta(n^2) swaps. This is worse than O(n*log(n))!

Posted: **Fri Nov 04, 2011 10:26 pm**

So, swapping a block requires that the individual units be swapped?

Can the array be re-built to define the blocks as a single element? This would be Dependant upon all of the elements of the array being a fixed size, lets call it one "block"

IE:

reorganize()
for i from 1 to n-1

define (newarray) (Block 1 through Block i, Block i+1 through Block n, Block n+1 through Block 2n-1, Block 2n-i+1 through Block 2n)
swap(newarray; element 2 with element 3)

final step:
define (finalarray) (Block 1, Block 2, Block 3, .... Block 2n)

I'll think about it some more. Here I thought I had it whooped.

Posted: **Fri Nov 04, 2011 10:34 pm**

Copying a block of n elements takes asymptotically n times as long as copying a block of 1 element. It often times makes sense to use blocks to simplify the problem into a smaller subproblem that we can then recursively solve, but we still can't magically copy around a block of n elements in constant time.

My friend's solution, which uses blocks, still requires n swaps per round, but he only needs log(n) rounds.

Posted: **Fri Nov 04, 2011 10:37 pm**

Using your spreadsheet where you color in swapped elements, a good measure for the time required is what is the area of the colored cells. For instance, in your last spreadsheet, it looks like the area is about 2n * 1/2n = O(n^2).

Posted: **Fri Nov 04, 2011 10:56 pm**

Something that someone suggested to me is to look at the problem in terms of the permutation. We can define any permutation in terms of its "cycles." Sirius might be interested in this, since it seems to overlap with what he was suggesting.

For example, for n = 5, we have 10 elements.
We want to map 0->0, 1->2, 2->4, 3->6, 4->6, 5->1, 6->3, 7->5, 8->7, 9->9.
We can also define this permutation in terms of the following cycles:
0->0
1->2->4->8->7->5->1
3->6->3
9->9

So ignoring the two trivial cycles at the ends, we put 1 in 2, 2 in 4, 4, in 8, etc.; and then 3 in 6 and 6 in 3.

Swapping like this clearly only requires n swaps, but, pursuing this strategy, the problem is in calculating these cycles without blowing any of the space or time constraints.

Posted: **Sat Nov 05, 2011 2:35 am**

Bumped it up to 100 to see if I could spot any patterns there:
0->0
1->2->4->8->16->32->64->29->58->17->34->68->37->74->49->98->97->95->91->83->67->35->70->41->82->65->31->62->25->50->1
3->6->12->24->48->96->93->87->75->51->3
5->10->20->40->80->61->23->46->92->85->71->43->86->73->47->94->89->79->59->19->38->76->53->7->14->28->56->13->26->52->5
9->18->36->72->45->90->81->63->27->54->9
11->22->44->88->77->55->11
15->30->60->21->42->84->69->39->78->57->15
33->66->33
99->99

Unfortunately this still doesn't tell me enough to draw any conclusions from; I note that save the beginning and end numbers, all of them are products of no more than two of the set of 1 and the prime numbers 3, 5 and 11. What I'm not sure about is whether there's any rhyme or reason to that - 2 is skipped (as it will usually be except in the most trivial possible set), and so is 7.

I guess the only thing for it is more data, and preferably on sets that are as large as possible. Not always powers of 10, either, I think.

P.S. Also, all the above list except 5 and 15 are factors of 99 (not always prime factors, but still). Actually they're pretty much all the factors of 99. But I'm not sure where 5 fits into the puzzle; I know it's the other prime factor of 100 apart from 2 (2 * 2 * 5 * 5) but I also note it didn't show up in the 10 list.

P.P.S. Actually, not showing up in the 10 list is kind of obvious on retrospect - it's over the half-way mark, and only one of the numbers (the maximum index) shows up there by necessity. I still don't know I'm anywhere close to how to predict 5 though - the 15 is 3 * 5, but why is there no 3 * 3 * 5? More than two factors?

Posted: **Mon Nov 07, 2011 3:16 pm**

0 double 0
1(double) 2 (double) 4 (double) 8 (double) 16 (double) 32 (double) 64 (double +1 - 2n) 29 (double) 58 (double +1 - 2n) 17 (double) 34 (double) 68 (double + 1 - 2n) 37 (double) 74 (double +1-2n) 49 (double) 98 (double +1 -2n) 97(double +1 -2n) 95 (double +1 - 2n) 91->83->67->35->70->41->82->65->31->62->25->50->1 (it works all the way out, I think) I.E. if (i>n) then i+1=2i + 1 - 2n else i+1=2i until you get back to the seeded number.
3->6->12->24->48->96->93->87->75->51->3 again... seed at the first number not moved yet.
5->10->20->40->80->61->23->46->92->85->71->43->86->73->47->94->89->79->59->19->38->76->53->7->14->28->56->13->26->52->5
9->18->36->72->45->90->81->63->27->54->9
11->22->44->88->77->55->11
15->30->60->21->42->84->69->39->78->57->15
33->66->33
99->99

keep seeding until you run out of locations that haven't been moved. (or until the seed number is larger than 2n)

Posted: **Mon Nov 07, 2011 3:34 pm**

I don't have the time to figure out the code for this, but I'd be interested to see how you guys would write it.

As far as I can tell:

This requires a "spare" space that's one element large.

This will require 2n + c time, where c is the number of times you have to iterate the permutation (c comes from having to initially vacate the seed location).. where ideally you'd vacate the seed, then work the chain backwards until you got to the seed. from this, it wouldn't be quite O(n) time, but it would certainly be close.

Posted: **Mon Nov 07, 2011 8:12 pm**

snoopy wrote:again... seed at the first number not moved yet.

How do you know the first number not moved yet?

Posted: **Mon Nov 07, 2011 9:39 pm**

Yeah, that's the big question I haven't quite answered. The easiest way requires a non-constant number of variables (basically a bitmap of all the "moved" elements in the array).

Haven't yet taken the time to investigate this further though.

Posted: **Tue Nov 08, 2011 6:58 am**

I'm not seeing a nice pattern to the seed numbers. About the best I can think of is along the lines of what Sirius said, make a binary block that's 2n long, and set one's as you move locations.

Otherwise, if space is more important than time, you can iterate back through your seeds, and carry some sort of a "count" number, but that would really waste a lot of time. There's probably a way to predict the seed numbers necessary.

Posted: **Fri Nov 18, 2011 12:02 pm**

There we go.
For those of you that follow this forum in RSS ignore my last comment.

This does it!

Code: Select all

>>> [y[::-1] for y in sorted([x[::-1] for x in mylist])]

Posted: **Fri Nov 18, 2011 1:25 pm**

Isaac wrote:There we go.
For those of you that follow this forum in RSS ignore my last comment.

This does it!
Code: Select all
>>> [y[::-1] for y in sorted([x[::-1] for x in mylist])]

that isn't in-place.

Posted: **Fri Nov 18, 2011 2:55 pm**

Welp, 5min of typing up a practical solution:

Code: Select all

void test ( void )
{
    int
        i, j, k, t ;
    int
        x[] = { 11, 12, 13, 14, 21, 22, 23, 24 } ;
    int
        n = sizeof( x ) / sizeof( int ) ;

    for ( i = 1, j = n / 2 ; i < n - 1 ; i += 2, ++j )
    {
        t = x[i] ;
        x[i] = x[j] ;

        for ( k = j ; k > i + 1 ; --k )
            x[k] = x[k - 1] ;

        x[k] = t ;
    }
}

Posted: **Fri Nov 18, 2011 4:12 pm**

That algorithm is correct and in-place, but it takes \Theta(n^2) time.

Posted: **Fri Nov 18, 2011 10:05 pm**

Jeff250 wrote:That algorithm is correct and in-place, but it takes \Theta(n^2) time.

Jeff250 wrote:But if you're doing, on average, n/2 swaps on each of n rounds, then this is n*n/2 = \Theta(n^2) swaps. This is worse than O(n*log(n))!

If I get that right it's (n / 2) - 1 rounds w/ n / 2 swaps per (approx.) tho...

Posted: **Sat Nov 19, 2011 2:06 am**

It's still \Theta(n^2), asymptotically worse than O(n*log(n)).

Posted: **Sat Nov 19, 2011 1:51 pm**

fliptw wrote:
Isaac wrote:There we go.
For those of you that follow this forum in RSS ignore my last comment.

This does it!
Code: Select all
>>> [y[::-1] for y in sorted([x[::-1] for x in mylist])]
that isn't in-place.

Oh, then I misunderstood. I figured appending new data to "mylist" and running that line would do it perfectly each time. I guess I've never done an "in-place" module before, but if it's more than what I have there, I don't think I'll ever need one.

Posted: **Mon Nov 21, 2011 3:17 am**

Here's the solution:
http://arxiv.org/abs/0805.1598

It seems impractical to expect someone to be able to solve this during a phone interview, but the question was probably just to see how far you can get.

Here's some python code I wrote for it:

Code: Select all

# Usage:
# >>> example(6)
# ['a1', 'a2', 'a3', 'a4', 'a5', 'a6', 'b1', 'b2', 'b3', 'b4', 'b5', 'b6']
# >>> shuffle(example(6))
# ['a1', 'b1', 'a2', 'b2', 'a3', 'b3', 'a4', 'b4', 'a5', 'b5', 'a6', 'b6']

def reverse(list, i, j):
    while i < j:
        list[i], list[j] = list[j], list[i]
        i, j = i + 1, j - 1

def next(i, n):
    if 0 <= i < n:
        return 2 * i
    elif n <= i < 2 * n:
        return 2 * (i - n) + 1
    else:
        raise ValueError()

def cycle(initial, n):
    i = initial
    while True:
        i = next(i, n)
        yield i
        if i == initial:
            break

def shuffle(list):
    off = 0
    while off < len(list):
        length = len(list) - off
        n = length // 2
        k, power = 0, 1
        while power * 3 <= length:
            k, power = k + 1, power * 3
        m = (power + 1) // 2
        reverse(list, off + m, off + n + m - 1)
        reverse(list, off + m, off + 2 * m - 1)
        reverse(list, off + 2 * m, off + n + m - 1)
        power = 1
        for k in xrange(k):
            last = list[off + power]
            for i in cycle(power, m):
                list[off + i], last = last, list[off + i]
            power = power * 3
        off = off + 2 * m
    return list

def example(n):
    return [c + str(i + 1) for c in 'ab' for i in xrange(n)]

I think we were on the right track. In a nutshell, given 2*n elements, find the largest 2*m <= 2*n where you can, using some number theory, trivially find the cycles. Shift the array from [1..2n] into [1..m, n+1..n+m, m+1..n, n+m+1...2n] by calling reverse on three subintervals. Then trivially solve the first 2*m elements, and then recursively solve the remaining 2(n-m) elements. Given the worst case value of m, you can still do a linear number of operations to reduce the problem to a 1/3 of its original size, so you can still solve it in T(n) = k*n + T(n/3) = O(n) time.

Posted: **Mon Nov 21, 2011 7:41 am**

Jeff250 wrote:Here's the solution:
http://arxiv.org/abs/0805.1598

It seems impractical to expect someone to be able to solve this during a phone interview, but the question was probably just to see how far you can get.

I think you're right. The goal probably isn't really to see the person find an answer (since it isn't trivial) - it's to see that the person has a familiarity with the concepts and to see how they would approach solving a difficult problem.

I've had a few classes about management that have covered hiring. One of the the biggest goals in an interview is to figure out a little bit of how the person's inner workings tick.... I bet this problem does a decent job of revealing this.

Posted: **Mon Feb 13, 2023 10:15 pm**

I thought it would be fun to revisit this and see what chatgpt would come up with.

Chatgpt:

Yes, there is an O(n) algorithm to solve this problem. Here's one approach:

Iterate over the array from left to right, and for each pair of elements (a_i, b_i), swap b_i with the element immediately to its right (a_{i+1}).
Iterate over the array from left to right, and for each pair of elements (a_{2i-1}, a_{2i}), swap a_{2i} with the element immediately to its right (b_{2i}).
Repeat steps 1 and 2 until the entire array is in the desired order.
This algorithm works by swapping each pair of elements in-place, and since there are n/2 pairs, each iteration of steps 1 and 2 takes O(n) time. Since the number of pairs is halved in each iteration, the algorithm takes O(log(n)) iterations, for a total running time of O(n log(n)).

It's worth noting that this algorithm is essentially the same as the one your friend gave, but with the difference that it performs each iteration in a single pass over the array, rather than recursively breaking it up into smaller blocks.

Here's one way to implement the algorithm in Python:

Code: Select all

def reorder_array(arr):
    n = len(arr) // 2
    for i in range(n):
        arr[2*i+1], arr[n+i] = arr[n+i], arr[2*i+1]
    for i in range(n-1):
        arr[2*i+2], arr[n+i+1] = arr[n+i+1], arr[2*i+2]
    if n > 1:
        reorder_array(arr[:n*2])

Here, arr is the input array. The function reorder_array takes the array as an argument and modifies it in place to reorder the elements. The first two for loops perform the swapping of elements as described in the algorithm. The if statement checks whether there are at least two pairs of elements in the array (i.e., whether n > 1), and if so, recursively calls the reorder_array function on the first n*2 elements of the array (i.e., the pairs of elements that were just swapped).

Note that this implementation assumes that the length of the input array is even, since the array is partitioned into pairs of elements. If the length of the array is odd, the algorithm will still work, but the last element of the array will be left in its original position.

DescentBB

Challenge

Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge

Re: Challenge